Calcolo dei limiti

Il quinto punto nello studio di una funzione è il calcolo dei limiti. Il calcolo dei limiti ci serve per determinare la direzione della curva negli estremi degli intervalli. Il limite è un operazione matematica con cui si assegnano tutti gli estremi non compresi di ogni intervallo del dominio alla variabile indipendente x. vediamo un esempio di limite.

questo è un limite la variabile x tende alla variabile c che può essere presa sia da sinistra che da destra ( un esempio per capire meglio cosa significa da sinistra e da destra ; per esempio abiamo il numero 5 da sinistra significa che non sarà 5 ma 4,9999 invece da destra sara 5.0001 quindi è quasi 5 ma non 5 e ci avviciniamo o da sinistra cioè per valori piu piccoli o da destra quindi per valori piu grandi) di f(x) cioè la nostra funzione il risultato è + o - infinito. questo ci fa capire che la funzione arriverà all'estremo c in piu infinito. proviamo a capire tutto ciò in un esercizio, anzi continuiamo l'esercizio che abbiamo visto nello studio del segno. Riecco la funzione:

---

il suo dominio era :

  

eravamo rimasti al segno della funzione e il grafico che avevamo disegnato era questo:

e il grafico dello studio del segno era questo:

ora guardando il dominio della nostra funzione calcoliamoci i limiti :

iniziamo col guardare quali sono gli estremi non compresi sono :     N.B. il limite di -7/4 va calcolato sia da sinistra che da destra.

Iniziamo col limite tendendente a :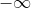

in questo limite abbiamo trovato una forma indeterminata,che cosa significa? è un limite che si risolve attraverso processi molto complicati, per semplificarci le cose basta seguire una semplice regola 

avendo un limite tendente a infinito per calcolare il suo risultato basta vedere l'ordine del numeratore e del denominatore per esempio: 

• se il numeratore è di grado maggiore del denominatore il risulato che otterremo sarà 
• se il denominatore è di grado maggiore del numeratore il risultato che otterremo sarà 0
• se invece il numeratore e il denominatore sono dello stesso grado il risultato sarà il rapporto tra i coefficienti di grado maggiore.

Ora calcoliamo il limite tendente a -7/4 da destra e da sinistra:

in questo limite notiamo che un numero intero fratto un infinitesimo (uno zero positivo o negativo) come risultato otterremo un infinito il cui segno sarà calcolato con il prodotto dei segni del numeratore e del denominatore.

Calcoliamo l'ultimo limite cioè quello tendente a :

---

Il calcolo dei limiti è stato completato e sappiamo cosa ci permettono di fare nello studio di una funzione.Ma i limiti permettono anche un altra cosa,i limiti servono a calcolare gli asintoti che possono essere 

• orizzontali 
• verticali 
• obliqui

ma li vedremo nella prossima lezione che sarà la ricerca degli asintoti.